Interior ballistic model, Powder modeling & Sources
Interior Ballistic Model
The interior ballistic model used in the GRT is a custom development on the basis of the information given in the book “Waffentechnisches Taschenbuch” by Rheinmetall1), in the books “Ballistik - Theorie und Praxis” by Beat P. Kneubuehl2), as well as “Ballistik” by Richard Emil Kutterer3) and also be influenced by IBHVG2 “lumped-parameter model”4).
Different burning characteristics
The various propellants or powders have different burning characteristics, i.e. depending on the manufacturer and type, the powder burns at different speeds during pressure development! Such powders behave either progressive, degressive or a specific combination of both. The traditional terms used to advertise powder behavior – e.g. “progressive” and “offensive” do not contradict this, because even offensive powders can be very progressive.
To differentiate burn behavior for propellant selection, creates opportunities to increase projectile acceleration in a longer barrel and keep pressures low at the same time.
Form functions & mapping
 This powder burn-up characteristic is mathematically simulated in the simulation calculation
by so-called form functions. This form function mathematically represents and approximates
the behaviour of the powder during the burning process.
This powder burn-up characteristic is mathematically simulated in the simulation calculation
by so-called form functions. This form function mathematically represents and approximates
the behaviour of the powder during the burning process.
The mathematical representation of a powder characteristic is based on a standardized measurement, e.g. with a calorimeter bomb or closed vessel (pressure bomb / manometric bomb), which has a specific volume. Several measurements are then taken and recorded with a fixed test quantity delta of a propellant powder.
The parameters of the form functions are changed so that they model the measurement curve. Subsequently, a calibration with ballistic data must be performed, because the propellant can act differently in the dynamic behavior of a gun.
 After adaptation and calibration, the mathematical representation does not necessarily
correspond to the original measurement data, since the propellant charge behaves dynamically
differently than in the static closed vessel. Without a closed vessel measurement, it is possible
to create an reengineered model using ballistic data including pressure equipment directly on the barrel
over a calibre spectrum and bullet weights.
After adaptation and calibration, the mathematical representation does not necessarily
correspond to the original measurement data, since the propellant charge behaves dynamically
differently than in the static closed vessel. Without a closed vessel measurement, it is possible
to create an reengineered model using ballistic data including pressure equipment directly on the barrel
over a calibre spectrum and bullet weights.
The closed vessel measurement is therefore one of the most important initial data for a powder model. As a rule, powder manufacturers perform this measurement for research and quality control purposes.
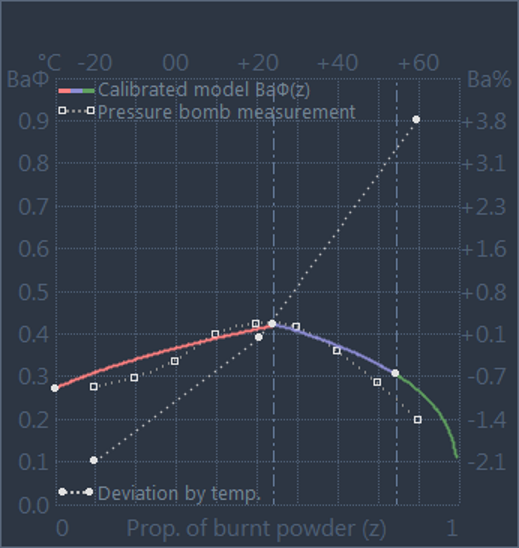
The value Ba given in the powder data is the start of this curve, which is composed of two or more sections. In contrast to the other software, GRT has a three-step representation of the burn-up behavior which accounts for multi base propellant behaviors and partially for additives of propellants nowadays like anti-copper-fouling and temperature-stabilizers etc.
Determination of powder characteristics
The calculations of internal ballistics depend on these powder characteristics. To determine the powder characteristics there is either the possibility of thermodynamic calculation 5), or experimental determination. The experimental determination of most powder characteristics can be performed using a closed vessel (manometric bomb).
The Closed Vessel
Pressure in the closed vessel (manometric bomb)
The basic idea behind the closed vessel is that a certain amount of propellant powder mc is burnt in a fixed volume V_mb. At combustion a maximum pressure p_mb depending on powder and quantity is reached.
p_mb * ( V_mb - b * mc ) = mc * R * T_ex
mc is the powder mass, b is the covolume, R the gas constant and T_ex the explosion temperature (flame temperature) of the combustion gases (usually calculated thermodynamically).
Powder constant, specific energy
The specific energy F_se is obtained from the product of gas constant R and explosion temperature T_ex:
F_se = R * T_ex
This specific energy represents the pressure energy during the burning of the powder, which is available for conversion into mechanical energy.
Abel's equation
The English chemist F. A. Abel released investigations and an equation published in 1874, proposing to use the general equation of state at high pressures. This is the reason, why the Van-der-Waals equation are not used here. In the case of conditions occurring in ballistics and explosives, the intrinsic volume of the gas molecules must be also considered (covolume b). If the charge density delta is calculated from the ratio of powder mass mc and combustion chamber V_mb (mc/V_mb), the equation known in ballistics as Abel's equation is obtained:
p_mb = (delta * F_se) / (1 - delta * b)
Measurements
Charge density in the combustion chamber of a manometric bomb must not exceed a maximum value in order to achieve uniform combustion from measurement to measurement and thus an evaluable pressure curve. The maximum value itself depends on the specific explosion heat Qex of the powder used. After the investigations of Gallwitz experience has shown that about delta * Qex = 545 kcal/dm³ has to be.6)
Raw data & processing
In practice, however, due to ubiquitous and unavoidable scattering, measurements must be carried out with different charge densities. Specific energy and covolume are then determined by linear regression. The reciprocal values of the measurements performed form pairs of values. The slope of the regression line gives the reciprocal of the specific energy F_se, from which the covolume b can be determined.
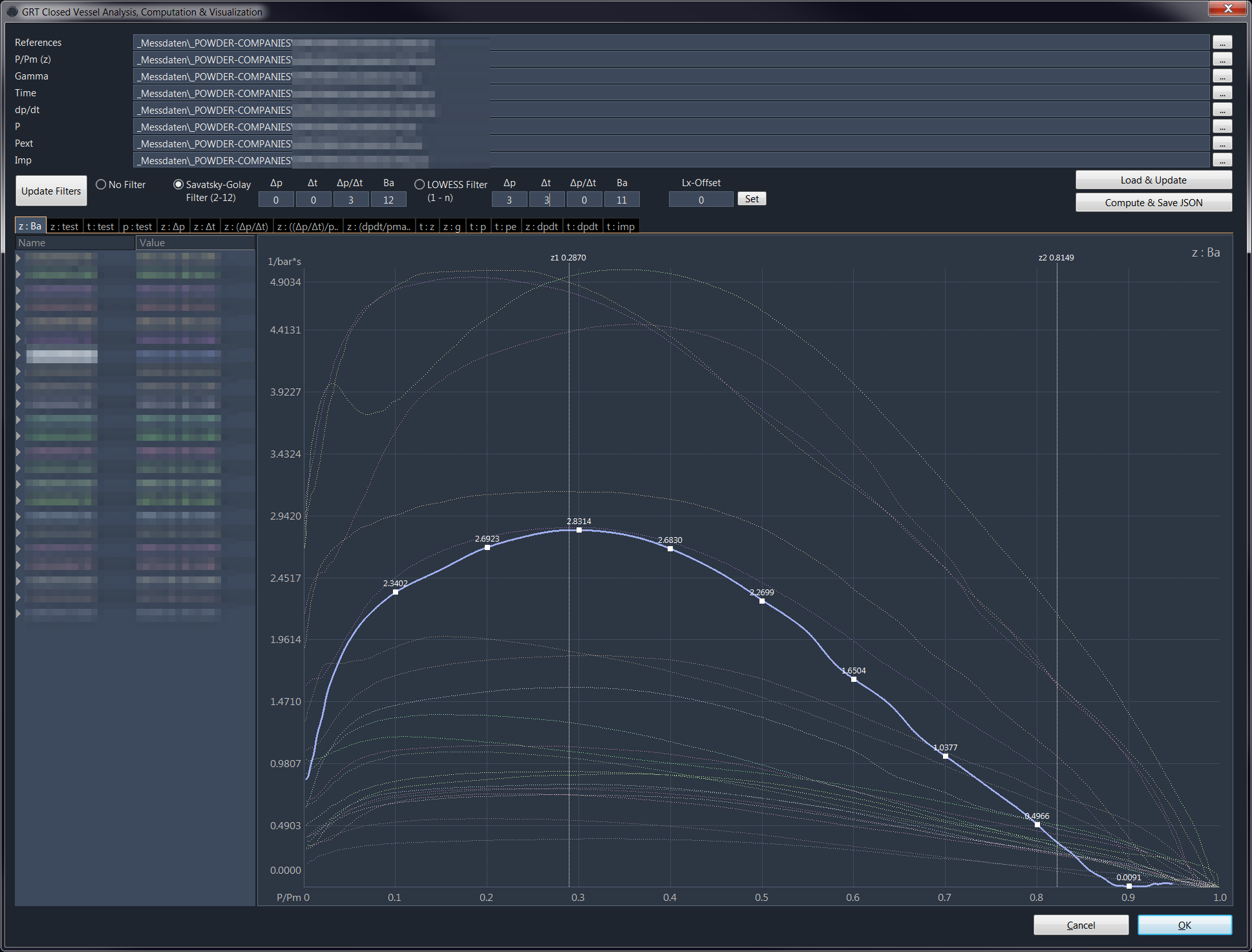
In the measurement, the pressure is recorded as a function of time, where z(t) is the proportion of the converted charge. As said, the problem here is the unavoidable scattering and noise of the signal:
The recorded data is analysed & processed aftermath e.g. using filters like Savatsky-Golay or LOWESS. The results can vary dependent on the filters and parameters used. That is the reason why the values used in a GRT powder model can be slightly different from the figures published by the manufacturer, because the manufacturer may use different filters or parameters for theyr analysis.
If the law of combustion is used instead of z(t), it can be resolved according to the product of dynamic vivacity and form function phi(z) (see image/diagram above, Y-axis).
( Ba * phi(z) ) / p0 = (ppunkt(t) / p(t)) * ( (1- b*z(t)*delta - (1-z(t))*delta/pc)² / (delta * F_se * (1-delta/pc)) )
b is the covolume, delta the ratio of powder mass and combustion chamber mc/V_mb and pc the density (mass density) of the powder substance.
Temperature Influence on Propellants
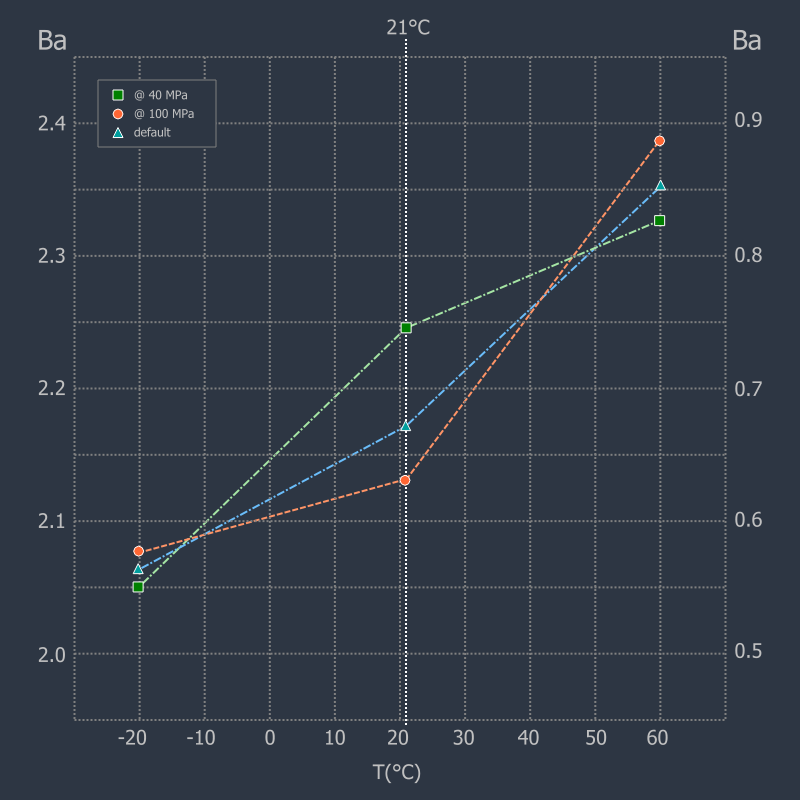 In the GRT, the change in the combustion behaviour due to the influence of powder
temperature is represented by temperature coefficients, which separately represent
the range below and above the default temperature of 21°C (see picture on the right,
not to scale).
In the GRT, the change in the combustion behaviour due to the influence of powder
temperature is represented by temperature coefficients, which separately represent
the range below and above the default temperature of 21°C (see picture on the right,
not to scale).
The user has the possibility to change the propellant temperature from the default value within a limited range in order to take account of environmental influences.
In general, the temperature drift of the propellants is represented by generally accepted analyses and algorithms. 7) 8) 9) 10) Some manufacturers give temperature coefficients from specific measurements for their propellant powders, which improves the results, otherwise the internal default coefficients are used.
To determine the coefficients, the vivacity measurements are repeated at a given temperature and then calculated as follows:
Cold Temperature Coefficient (tcc)
tcc = (Ba(T= +21°C) - Ba(T= -20°C)) / (21+20)
Hot Temperature Coefficient (tch)
tch = (Ba(T= +60°C) - Ba(T= +21°C)) / (60-21)
Energies at the shot
The chemical energy released by the conversion of the propellant charge is essentially divided into the following quantities when the shot is fired:
- The translational projectile energy
- The rotational projectile energy
- Flow energy of the powder gases
- Internal energy of the powder gases
- Heat losses at tube, bullet and sleeve
- Gas losses, friction and acoustics (vibration behavior)
- the work against the pull-out resistance
- The work of pressing the bullet into the lands
- Energy of the recoiling weapon parts
- Energy for cycling (semi-)automatic weapons
Losses
The friction losses on the projectile are represented in the algorithm by models, where frictional resistances are primarily specified by the bullet manufacturer if available. The experienced user is given the possibility of manual adjustment.
The flow energy of the powder gases can be calculated by adding a proportion of the charge (carrying factor, “Sebert-factor”) to the bullet mass to be accelerated. As is usual in other areas of physics, an effective mass is calculated. Also other energy losses can be considered here in the effective mass, e.g. the energy losses by heat input.
The gas losses due to constructive conditions such as the cylinder gap of revolvers can amount to up to 20%. They can be specified by the experienced user with the help of a wizard.
The portion of the gun recoil, as well as the propulsion energy of automatic weapons is neglected.
Data
The caliber, bullet and propellant powder data provided by the GRT are laboriously created by the GRT development team and the community and manually entered data, whereby the data of the propellant powders are based on the measurement data provided by the respective manufacturers, as well as data which have been and will be determined by GRT laboratory and the community on the basis of its own measurements.
Special thanks go to the companies (in alphabetical order):
Important note
Due to manufacturing fluctuations and tolerances, it is important to compare the data provided with the real conditions and adjust them if necessary. In particular: case volume and bullet length must always be checked and measured. No guarantee is given for the correctness of the data provided!